David Mertz, Ph.D.
Gnosis Software, Inc.
September 2001
This paper extends its author's earlier research into compression of XML documents. The special structures in XML tend to allow certain improvements over the most naive compression techniques--some lossless document restructuring techniques can serve to improve compression ratios. For a certain class of applications, however, document-level restructuring/compression is not practical. This paper explores adaptation of restructuring techniques to streaming channels, using block-level algorithms. Code exploring these techniques is provided in the paper, along with representative quantitative results.
Introduction
XML documents, as is well known, tend to be quite large compared to other forms of data representation. Of course, in balance to this, the simplicity and generality of XML makes it worthwhile, despite its verboseness. Much of the time, in fact, the size of XML really makes no difference--DASD is cheap, and the time on the wire might be only a small part of the total time in the process. But at other times, bandwidth and storage space can be important.
To quantify matters, it is not at all unusual for XML documents that represent table-oriented data to be three times as large as a CSV or database representation, or even than a flat file. A similar increase is typical in representing EDI data (such as for ebXML projects). In many of these context, one starts out with multi-megabyte data sources, and making them multiple times larger can be inconvenient, especially for transmission purposes. For example, for purposes of my research, I created an XML representation of an approximately 1 megabyte Apache access logfile. This created an XML document 3.18 times the size of the underlying line-oriented log. The only information added in the process was some descriptive names for fields that could have also been specified in a single header line of less than a hundred bytes. Moreover, my specific XML representation did not include any namespaces in the tags, which would have increased the size further.
Prior Results
Some of the inspiration for my efforts comes from the work of the XMill XML compressor (see Resources). However, the similarity of the work presented here to that in XMill is only at a general conceptual level. No effort was made to obtain file compatibility, nor did I closely examine the source code or algorithms in XMill. Moreover, all the code presented in this paper--and in any earlier or later research I do into the topic--is released to the public domain. Furthermore, as far as I know, these concepts are unencumbered by any patents.
The high-level idea that I work with is the fact that XML
documents tend to be composed of intermixed data elements,
where elements of the same tag-type typically have semantically
related contents. Or more specifically, element bodies
enclosed by the same tag tend to have recurrent substrings.
For example, the XML weblog used as a sample document in the
below results contains a <host> element that contains IP
addresses. But each <host> element is separated from others
by various elements that do not contain IP addresses.
Lempel-Ziv style compression algorithms, in particular, take
the strongest advantage of documents where recurrent strings
occur relatively close together (the dictionary remains intact
between occurrences). If one could restructure an XML document
so that elements of the same type occur adjacent to each other,
these restructured documents are likely to be more
compressible (using pre-existing tools).
The Burrows-Wheeler compression algorithm is used by the
utility bzip2, and by the library versions of the same code.
Burrows-Wheeler performs something quite a bit similar to the
restructuring presented in this paper, but at a level of
generality that allows it to operate on all document types, not
only XML. The strategy of bzip2 is to automate the
identification of "similar" strings within a file, and compress
based on identified similarities. bzip2 almost always
obtains significantly better compression ratios than do
Lempel-Ziv based utilities like gzip, but at the cost of
considerably slower performance.
I found in my earlier research (see Resources) that a custom
XML-specific (lossless) document restructuring can improve
subsequent compression. If the subsequent compression if based
on gzip the improvement in compression ratio is consistent,
and is often better than 30%. If the subsequent compression is
based on the far superior bzip2 utility, restructuring prior
to compression can range anywhere from a very slight decrease
in compression ratio to a bit better than a 10% improvement.
The quick moral is that Burrows-Wheeler is an awfully good
algorithm to start with. But if speed is crucial (i.e. you
want gzip) or squeezing out that last byte is important for
channel/storage costs, a restructuring approach can be used
with bzip2.
My initial research, however, only looked at file-level operations--for both restructuring and compression. If one must deal with multi-megabyte XML documents, spending the memory, disk space, and CPU overhead to manipulate huge documents is often impractical. What would be nice would be if one could take not the entire multi-megabyte source, but only parsed blocks read serially, and apply similar techniques. Moreover, the effectiveness of the Burrows-Wheeler algorithm depends in large part on being able to make global manipulations on large inputs sources--we find in the below quantitative analysis that Burrows-Wheeler loses all its advantages when addressing (relatively) small serial blocks from XML documents. The restructuring-pass techniques retain their effectiveness to a much larger degree under this constraint.
Practical Application
There are a variety of practical purposes the restructuring/ compression techniques addressed in the paper can be put to. The very simplest case is one where XML files are relatively large (e.g. hundreds or thousands of megabytes), memory and disk-space moderately constrained (e.g. there are not gigabytes of extra memory/storage available for the process), and channel costs comparatively expensive (e.g. transmitting a half-gigabyte is a worthwhile savings over transmitting a gigabyte). The scenario for the simplest case would utilize a protocol like the below:
0. Machine A has both a channel to Machine B and a large XML
source (either a file or some dynamic generation of XML
content).
1. A SAX parser on A, "flushes" its data each time a block
worth of source XML has been encountered.
a. The flushed block is restructured.
b. The flushed block is compressed by conventional
means (i.e. 'gzip' or 'bzip2').
c. The restructured/compressed block is transmitted.
2. Machine B receives blocks over the channel. The
underlying XML is reconstructed in a serial fashion.
Each block of XML could be appended to a file; or it
could itself be fed to a SAX parser that acted on the
elements and contents (and discarded once processed).
|
At a slightly more "exotic" level one could imagine the restructuring/compression techniques implemented on routers, or on other embedded systems. The end points might never see anything other than plain XML, but internally to the packet routing, a more compact representation can be used. As more backbone traffic becomes devoted to XML content, this usage becomes more appealing. Of course, generic compression techniques implemented on routers could simply compress all traffic, albeit somewhat less efficiently in the case of XML documents.
One additional point can be noted, but is not quantitatively analyzed in this paper. By choosing block sizes for restructuring to match CPU architecture, one might achieve cache-hit efficiencies on block transformations. The block sizes used in the below analysis are within the range of primary, secondary, and tertiary caches of modern chip architectures. Further research will hopefully address cache/block size tradeoffs in a quantitative manner on various Intel chipsets (embedded and desktop).
An Overview Of The Technique
Very little in the restructuring technique needed to be changed from earlier work to accommodate arbitrary block sizes. In the original algorithm, a list of tags was included as the first delimited section of a restructured XML documents. This list of tags--generated on an ad hoc basis during the actual document parsing--was used as an index for single-byte tag placeholders used in a structure schematic. The strategy of using byte index value in the place of tags itself reduces the size of restructured documents somewhat, but also limits the algorithm to handling DTDs with fewer than 254 distinct tags.
Under the block-level revision below, we instead assume that a taglist is available independently. A utility function to create a taglist from a DTD is provided. Assuming both sides of the channel have the requisite DTD, everything works--shy of a DTD, and other format that specifies the order of tags works too.
The only significant revision needed was the addition of a new (first) delimited document section to indicate current element nesting. In the original, every start tag was paired to an end tag. But since XML documents are broken at arbitrary positions, it is necessary to record a stack of "open" elements at the point a block begins. The first block parsed has an empty field for this first section; subsequent ones are likely to have one or more bytes listing tag indexes that have not yet been closed.
The format of a restructured block is rather simple:
BLOCK FORMAT: 1. List of open tags. Each start tag is a single byte (w/ byte value >= 0x03); this list is pushed on to the taglist stack to match corresponding close tag bytes. 2. A section delimiter: 0x00 (the null byte) 3. A compact representation of the block document structure, where each start tag is represented by a single byte, and the occurence of content is marked by a 0x02 byte. A close tag is represented by a 0x01 byte, and must be back-matched to corresponding start tag. 4. Another section delimiter: 0x00 (the null byte) 5. The contents of all the elements indicated in the document structure schematic, grouped by element type. Each individual content item is delimited by a 0x02 byte, while the start of elements of a new type is delimited by a 0x01 byte (the last not strictly needed, but it makes reversing the transformation easier). |
In the code presented blocks are compressed using zlib, which
is the algorithm and library underneath the gzip utility.
Compressed blocks are prepended with a 4-byte (32-bit) number
indicating the size of the block to follow, then sent to
STDOUT. For testing purposes, STDOUT was directed to a file
whose size could later be examined. Since compressed blocks
will vary in size, a block size flag is necessary to determine
their extents, and are reasonably considered part of the
resultant size (this makes little difference to the results, in
any case).
Two limitations of the presented code should be noted. The first is purely a product of research implementation convenience. Element attributes are not handled by the current parser. This is primarily to make the presented code easier to follow, and adding like-attribute blocks would be a straightforward extension of the current technique, and are unlikely to appreciably affect compression or performance.
A second limitation is more consequential. Blocks are only
flushed when end tags are encountered. If the PCDATA content
of single elements are not consistently smaller than the block
size used, no enforcement of the block size is performed. For
example, a huge XHTML document that contained one big <pre>
element would not enforce any reasonable block size. It might
be possible to change this limitation--although doing so would
by inelegant within a SAX framework. However, there is little
point in lifting this, since reorganization will be
inconsequential for documents with element contents larger than
the block size (and should not be performed in general). The
one situation where a problem could arise is when an
implementing system has a hard limit on available memory, and
encounters a block too large to process.
In the normal case, input XML blocks will be slightly larger than the indicated block size, but once single-byte tag placeholders are substituted for tags, the resultant size will typically be slightly smaller than the block size. Moreover, once compression is applied to the block, the compressed block size will be considerably smaller than the input block size.
The Source Code
Presented below is fully functional Python source code for
restructuring and compressing XML documents. Input is taken
from STDIN (e.g. a redirected file), and output is sent to
STDOUT. Each block on STDOUT is prepended with a block size
flag to allow the receiver to split the blocks back apart. The
utility xml2stuctblocks.py may be run from the command line
as described, or its main class StuctBlockExtractor may be
used as a SAX content handler in a larger application (possibly
modified so something different is done with compressed blocks
than writing them to STDOUT).
Following the restructure/compression code is its reverse
operation. structblocks2xml.py may be run in a similar
manner from the command-line, or adapted as a component of a
larger application.
xml2structblocks.py
import sys import xml.sax from xml.sax.handler import * import zlib def encode_size(n): "Given an number < 2**32, return a 4-byte string representation" b1, r = divmod(n,16777216) b2, r = divmod(r,65536) b3, b4 = divmod(r,256) return ''.join(map(chr,[b1,b2,b3,b4])) class StructBlockExtractor(ContentHandler): """Create a special structure/content form of an XML document""" def __init__(self, taglist, blocksize=1000, compress=1): if len(taglist) > 253: raise ValueError, "More than 253 tags encountered" self.taglist = taglist # the tags occurring in DTD/document self.empty_contentdct() # dictionary of content lists self.blocksize = blocksize # minimum (& approx total) input block self.compress = compress # should we compress blocks self.readsize = 0 # how much of block read so far? self.prior_state = [] # the state when this block started def empty_contentdct(self): self.contentdct = {} # dictionary of content lists for tag in self.taglist: self.contentdct[tag] = [] def flushblock(self): outlst = [] # a list to hold output strings for name in self.prior_state: # write the stack state at beginning of block outlst.append(chr(self.taglist.index(name)+3)) self.prior_state = self.state[:] # set prior_state for next flush outlst.append(chr(0)) # section delimiter 0x00 outlst.append(''.join(self.struct)) # add the current structure list self.struct = [] # empty document structure for next block outlst.append(chr(0)) # section delimiter 0x00 for tag in self.taglist: # Write all content lists outlst.append(chr(2).join(self.contentdct[tag])) outlst.append(chr(1)) # delimiter between content types self.empty_contentdct() # empty contentdct for next block outstr = ''.join(outlst) # stringify the block output if self.compress: # compress the block (?) outstr = zlib.compress(outstr) outlen = len(outstr) # what size is the output block? sys.stdout.write(encode_size(outlen)) # write 32-bit block size flag sys.stdout.write(outstr) # write the final processed block self.readsize = 0 def startDocument(self): self.state = [] # stack for tag state self.newstate = 0 # flag for continuing chars in same elem self.struct = [] # compact document structure def endDocument(self): self.flushblock() def startElement(self, name, attrs): self.state.append(name) # push current tag self.newstate = 1 # chars go to new item # single char to indicate tag self.struct.append(chr(self.taglist.index(name)+3)) self.readsize += len(name) # approximate size of tag itself def endElement(self, name): self.state.pop() # pop current tag off stack self.newstate = 1 # chars go to new item self.struct.append(chr(1)) # 0x01 is endtag in struct self.readsize += len(name) # approximate size of tag itself if self.readsize > self.blocksize: self.flushblock() # might have filled input block def characters(self, ch): currstate = self.state[-1] if self.newstate: # either add new chars to state item self.contentdct[currstate].append(ch) self.newstate = 0 self.struct.append(chr(2)) # 0x02 content placeholder in struct else: # or append the chars to current item self.contentdct[currstate][-1] += ch self.readsize += len(ch) # size of element contents def getTagsFromDTD(dtd): taglist = [] # the tags in the DTD if hasattr(dtd,'read'): # file-like argument for DTD dtd_str = dtd.read() else: # DTD text passed in (hopefully) dtd_str = open(dtd).read() elems = dtd_str.split('<!ELEMENT') # each element (& attributes, containers) for elem in elems[1:]: # exclude stuff before first element taglist.append(elem.split()[0]) return taglist if __name__ == '__main__': parser = xml.sax.make_parser() taglist = getTagsFromDTD(sys.argv[1]) blocksize = int(sys.argv[2]) handler = StructBlockExtractor(taglist,blocksize) parser.setContentHandler(handler) parser.parse(sys.stdin) |
structblocks2xml.py
def structblocks2xml(s, taglist):
prior, struct, content = s.split(chr(0))
state = [taglist[ord(i)-3] for i in prior]
# stack for prior tag state
contentlist = [] # list-of-lists of content items
for block in content.split(chr(1)):
contents = block.split(chr(2))
contents.reverse() # pop off content items from end
contentlist.append(contents)
skeleton = [] # templatized version of XML
for c in struct:
i = ord(c)
if i >= 3: # start of element
i -= 3 # adjust for struct tag index offset
tag = taglist[i] # spell out the tag from taglist
state.append(tag) # push current tag
skeleton.append('<%s>' % tag)
# insert the element start tag
elif i == 1: # end of element
tag = state.pop() # pop current tag off stack
skeleton.append('</%s>' % tag)
# insert the element end tag
elif i == 2: # insert element content
tag = state[-1]
item = contentlist[taglist.index(tag)].pop()
item = item.replace('&','&')
skeleton.append(item) # add bare tag to indicate content
else:
raise ValueError, "Unexpected structure tag: ord(%d)" % i
return ''.join(skeleton)
def decode_size(s):
"Given a 4-byte string representation, return a number < 2**32"
return ord(s[0])*16777216+ord(s[1])*65536+ord(s[2])*256+ord(s[3])
def flagsize_blocks(s):
offset = 0
blocks = []
while offset < len(s):
blocklen = decode_size(s[offset:offset+4])
offset += 4
blocks.append(s[offset:offset+blocklen])
offset += blocklen
return blocks
if __name__ == '__main__':
import sys, zlib
from xml2structblocks import getTagsFromDTD
taglist = getTagsFromDTD(sys.argv[1])
structblocks = sys.stdin.read()
for block in flagsize_blocks(structblocks):
block = zlib.decompress(block)
xml_block = structblocks2xml(block,taglist)
sys.stdout.write(xml_block)
|
Quantifying Compression
For purposes of quantification, I work with the same two
representative XML documents addressed in my earlier research.
One document was a prose-oriented document, and XML version of
Shakespeare's Hamlet. The markup includes tags such as
<PERSONA>, <SPEAKER> and <LINE> which map fairly
naturally to the typographic forms one might encounter in a
printed copy. The second XML source document was created from
a one megabyte Apache log file, with XML tags used to surround
each field of the log file (and each entry). The tags used
were not particularly verbose, but the file still expanded to
about 3 megabytes.
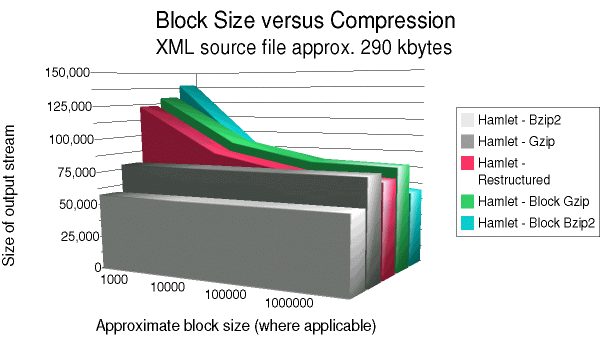
On the below graphs, the two gray bars in the front represent
the compression achievable with simple file-level compression,
using gzip and bzip2. As discussed above file-level
compression of large files might be impractical; but as
expected, file-level compression achieves better results since
it has the whole file to look for repeated strings in. In
general, one has to get up to blocks of 100 kilobytes or
larger before the block-level compression pulls nearly even
with the file-level compression. Still, if one has to worry
about gigabyte source documents, even a megabyte block looks
pretty manageable in comparison.
The green and blue bars at the back of the graph represent the
compression achievable by compressing blocks without a
restructuring pass. The gzip results use a prepended 4-byte
size flag, just as does the xml2structblocks.py. The bzip2
results simply concatenate the output of multiple calls to the
command-line bzip2 utility. This is done because no
post-alpha Python binding was available for the bzip2 library.
The result is to add a 10-byte header for each block output
(and makes it more difficult to reverse the transformation,
which is not important for the test). This does not have any
meaningful significance to the comparison.
Finally, the red bar in the middle represents the compression
performance of xml2structblocks.py. This utility uses zlib
library compression. Better compression results would be
obtained by using the bzip2 library. This was not tested,
however, both because of the lack of a Python binding, and
because most anticipated future uses are likely to make the
speed disadvantage of bzip2 prohibitive. However, if bandwidth
is more important than CPU time, adding a bzip2 compression
layer might enhance the benefits.
Let us look at the results, then make some comments. Block sizes of 1k, 10k, 100k, and 1M were tried. First Hamlet:

Large hamlet.xml compression graph: http://gnosis.cx/publish/programming/hamlet_compression_large.gif
Then a weblog:
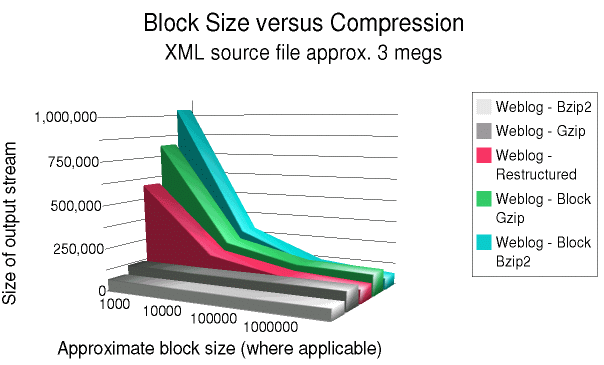
Large weblog.xml compression graph: http://gnosis.cx/publish/programming/weblog_compression_large.gif
The same general pattern occurs in both the hamlet.xml and
weblog.xml--but the pattern is much stronger in
weblog.xml (the highly repetitive structure of a log file
gives restructuring its strongest advantage). At small block
sizes, compression is much worse than file-level compression.
Around 10k block size, block-level compression starts to look
moderately good; and at 100k block size it becomes very close
to the file-level compression techniques.
The aspect of the charts that is most interesting for this
paper is the compression characteristics of the restructuring
block strategy. Restructuring consistently improves on the
behavior of simple block-level zlib (around 30% for the web
log, less for Hamlet). At around 100k blocks, restructuring
does better than file-level gzip, which is a very positive
result.
A surprising result is the behavior of block-level bzip2
compression. As one would expect, once block size gets large,
it makes no difference that block-level compression is used.
But one has to get to the 1m size to wipe out the whole
difference. However, at small block sizes (1k especially, but
even at 10k), block-level bzip2 does shockingly badly. Prior
restructuring is unlikely to improve this signicantly. In
fact, for the 1k block size bzip2 is consistently much worse
than zlib.
For reference, the exact file sizes graphed are below:
288754 hamlet.xml 57522 hamlet.xml.bz2 78581 hamlet.xml.gz 120794 hamlet.blocks-re-1000 87775 hamlet.blocks-re-10000 75284 hamlet.blocks-re-100000 71970 hamlet.blocks-re-1000000 129706 hamlet.blocks-z-1000 94423 hamlet.blocks-z-10000 81664 hamlet.blocks-z-100000 79707 hamlet.blocks-z-1000000 139628 hamlet.blocks-bz-1000 83994 hamlet.blocks-bz-10000 63475 hamlet.blocks-bz-100000 57503 hamlet.blocks-bz-1000000 3021921 weblog.xml 66994 weblog.xml.bz2 115524 weblog.xml.gz 563133 weblog.blocks-re-1000 188562 weblog.blocks-re-10000 107362 weblog.blocks-re-100000 83152 weblog.blocks-re-1000000 817730 weblog.blocks-z-1000 236383 weblog.blocks-z-10000 141154 weblog.blocks-z-100000 128120 weblog.blocks-z-1000000 1035478 weblog.blocks-bz-1000 278658 weblog.blocks-bz-10000 111476 weblog.blocks-bz-100000 68367 weblog.blocks-bz-1000000 |
Conclusion
The structure of documents significantly affects their compressibility with standard compression algorithms. Since XML encodes much detail of its semantic structure in its syntactic form, a "restructuring" of such documents can improve their compressibility. Moreover, this paper has shown that such restructuring techniques are amenable to serialization using parsed blocks from large XML documents. Potentially, if other performance features can be shown to be satisfactory, the transmission of large XML data flows can be fit into narrower bandwidths than a naive approach allows.
Resources
The writeup of my first round of research addresses document restructuring in a general way, without yet considering serialization issues. A number of quantitative comparisons are contained therein that provide useful background. The earlier article appears on IBM developerWorks (use its search facility). An archival copy can be found at:
http://gnosis.cx/publish/programming/xml_matters_13.html
The XMill XML compressor addresses XML document restructuring in a manner similar to that I have. Information and a downloadable version can be found at the below link. The license requires a click-through, and the download page unfortunately seems to have a buggy script that does not allow downloads from all sites.
http://www.research.att.com/sw/tools/xmill/
The complete plays of Shakespeare can be found in XML form at
the below resource. The document hamlet.xml used for testing
purposes was obtained there:
http://www.ibiblio.org/xml/examples/shakespeare/
The 1994 paper A Block-sorting Lossless Data Compression
Algorithm, by M. Burrows and D.J. Wheeler, introduced the
algorithm known now as Burrows-Wheeler. This technique is
implemented in the fairly popular bzip2 utility:
http://gatekeeper.dec.com/pub/DEC/SRC/research-reports/abstracts/src-rr-124.html
Many Unix-like systems include bzip2 as part of their
standard distribution. For other platforms--or for newer
versions--'bzip2' can be found at:
http://sources.redhat.com/bzip2/
I wrote what I believe is a good general introduction to data compression. It can be found at:
http://www.gnosis.cx/publish/programming/compression_primer.html